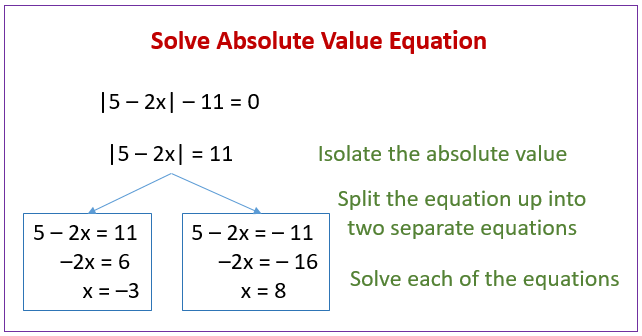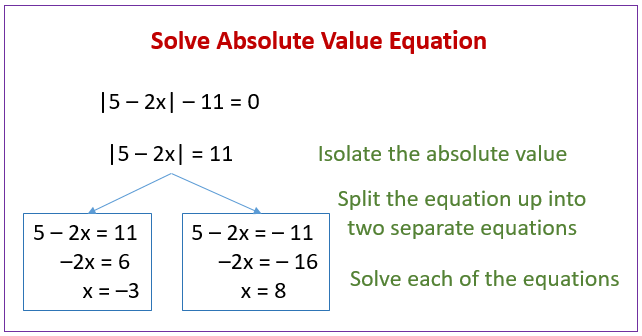Absolute Value Equation Worksheets

Examples, solutions, videos, and worksheets to help Grade 7 and Grade 8 students learn how to solve absolute equations.

How to solve absolute value equations?

There are four sets of simplifying algebraic expression worksheets.

To solve absolute value equations, you need to consider two cases: one where the expression inside the absolute value is positive and one where it is negative. Here’s a step-by-step guide on how to solve absolute value equations:

  1. Write the absolute value equation in the form |expression| = constant.
  2. Set up two separate equations, one with the expression inside the absolute value as positive and one with it as negative.
  3. Solve both equations for the variable.
  4. Check your solutions to ensure they satisfy the original absolute value equation.

Let’s go through an example to illustrate the steps:

Example: Solve the absolute value equation |2x - 5| - 13 = -6.

  1. Write the absolute value equation in the required form:
    |2x - 5| = 7
  2. Set up two separate equations:
    Case 1: 2x - 5 = 7
    Case 2: 2x - 5 = -7
  3. Solve both equations:
    Case 1: 2x - 5 = 7
    x = 6
    Case 2: 2x - 5 = -7
    Subtract 5 from both sides:
    x = -1
  4. Check the solutions:
    Substitute x = 6 into the original equation:
    |2(6) - 5| - 13 = |12 - 5| - 13 = |7| - 13 = -6 (True)
    Substitute x = -1 into the original equation:
    |2(-1) - 5| - 13 = |-2 - 5| - 13 = |-7| - 13 = -6 (True)
    Both solutions, x = 6 and x = -1, satisfy the original absolute value equation |2x - 5| - 13 = -6.
    So, the solutions to the absolute value equation are x = 6 and x = -1.

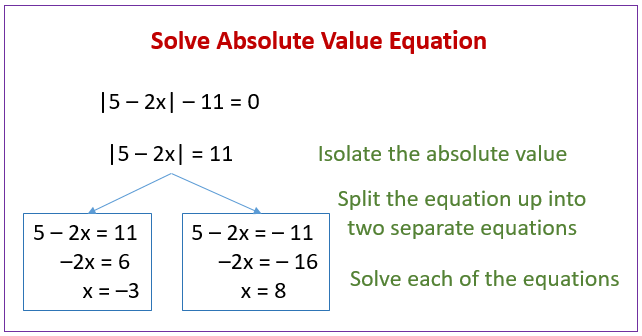
Absolute Value Equation

The following diagram shows another example of solving an absolute value equation.

Click on the following worksheet to get a printable pdf document.
Scroll down the page for more Absolute Value Equation Worksheets.